
“quote TBD”
Let’s take a moment to think back to a simpler time, when you wrote your first p5.js sketches and life was free and easy. What is one of programming’s fundamental concepts that you likely used in those first sketches and continue to use over and over again? Variables. Variables allow you to save data and reuse that data while a program runs. This, of course, is nothing new to you. In fact, you have moved far beyond a sketch with just one or two variables and on to more complex data structures—variables made from custom types (classes) that include both data and functionality. You've made your own little worlds of movers and particles and vehicles and cells and trees.
In each and every example in this book, the variables of these objects have to be initialized. Perhaps you made a whole set of particles with random colors and sizes or a list of vehicles all starting at the same x,y position. What if, instead of acting as “intelligent designers,” assigning the properties of the objects through randomness or thoughtful consideration, you could let a process found in nature—evolution—decide for you.
Can you imagine that the variables of a JavaScript object are its DNA? Can those objects give birth to other objects and pass down their DNA to a new generation? Can a p5.js sketch evolve?
The answer to all these questions is yes. After all, the book would hardly be complete without tackling a simulation of one of the most powerful algorithmic processes found in nature itself. This chapter is dedicated to examining the principles behind biological evolution and finding ways to apply those principles in code.
It’s important for me to clarify the goals of this chapter. I will not go into depth about the science of genetics and evolution as it happens in the physical world. I won’t be making Punnett squares (sorry to disappoint) and there will be no discussion of nucleotides, protein synthesis, RNA, and other topics related to the biological processes of evolution. Instead, I am going to look at the core principles behind Darwinian evolutionary theory and develop a set of algorithms inspired by these principles. I don’t care so much about creating a scientific accurate simulation of evolution; rather, I care about methods for applying evolutionary strategies in software.
This is not to say that a project with more scientific depth wouldn’t have value, and I encourage readers with a particular interest in this topic to explore possibilities for expanding the examples provided with additional evolutionary features. Nevertheless, for the sake of keeping things manageable, I'm going to stick to the basics, which will be plenty complex and exciting.
The term “genetic algorithm” refers to a specific algorithm implemented in a specific way to solve specific sorts of problems. While the formal genetic algorithm itself will serve as the foundation for the examples in this chapter, I won't make a fuss about implementing the algorithm with perfect accuracy given that I am looking for creative applications of evolutionary theory in code. This chapter will be broken down into the following three parts (with the majority of the time spent on the first).
While computer simulations of evolutionary processes date back to the 1950s, much of what have become commonly referred to as genetic algorithms (also known as “GAs”) today was developed by John Holland, a professor at the University of Michigan, whose book Adaptation in Natural and Artificial Systems pioneered GA research. Today, genetic algorithms are part of a wider field of research, often referred to as "Evolutionary Computing."
To help illustrate the traditional genetic algorithm, I am going to start with monkeys. No, not our evolutionary ancestors. I'm going to start with some fictional monkeys that bang away on keyboards with the goal of typing out the complete works of Shakespeare.

The “infinite monkey theorem” is stated as follows: A monkey hitting keys randomly on a typewriter will eventually type the complete works of Shakespeare given an infinite amount of time. It’s a theory because in practice the number of possible combinations of letters and words makes the likelihood of the monkey actually typing Shakespeare minuscule. To put it in perspective, even if the monkey started typing at the beginning of the universe, the probability of it producing “Hamlet,” let alone the entire works of Shakespeare, by now is still absurdly unlikely.
Consider a monkey named George. George types on a reduced typewriter containing only twenty-seven characters: twenty-six letters and one space bar. So the probability of George hitting any given key is one in twenty-seven.
Next, consider the phrase “to be or not to be that is the question” (I'm simplifying it from the original “To be, or not to be: that is the question”). The phrase is 39 characters long. If George starts typing, the chance he’ll get the first character right is 1 \text{ in } 27. Since the probability he’ll get the second character right is also 1 \text{ in } 27, he has a 1 \text{ in } 27\times27 chance of landing the first two characters in correct order—which follows directly from our discussion of "event probability" in the Introduction. Therefore, the probability that George will type the full phrase is:
(1/27) multiplied by itself 39 times, or (1/27)^{39}
which equals a probability of…
1 \text{ in } 66,555,937,033,867,822,607,895,549,241,096,482,953,017,615,834,735,226,163
Needless to say, even hitting just this one phrase, not to mention an entire play, is highly unlikely. Even if George were a computer simulation and could type one million random phrases per second, for George to have a 99% probability of eventually getting it right, he would have to type for 9,719,096,182,010,563,073,125,591,133,903,305,625,605,017 years. (Note that the age of the universe is estimated to be a mere 13,750,000,000 years.)
The point of all these unfathomably large numbers is not to give you a headache, but to demonstrate that a brute force algorithm (typing every possible random phrase) is not a reasonable strategy for arriving randomly at “to be or not to be that is the question.” Enter genetic algorithms, which will demonstrate that the process of starting with random phrases and find the solution through simulated evolution.
Now, it’s worth noting that this problem (arrive at the phrase “to be or not to be that is the question”) is a ridiculous one. Since you know the answer, all you need to do is type it. Here’s a p5.js sketch that solves the problem.
let s = "to be or not to be that is the question"; console.log(s);
Nevertheless, it’s a terrific problem to start with since having a known answer will allow you to easily test the code and evaluate the success of the genetic algorithm. Once you've successfully solved the problem, you can feel more confident in using genetic algorithms to do something actually useful: solving problems with unknown answers. This first example serves no real purpose other than to demonstrate how genetic algorithms work. If you test the GA results against the known answer and get “to be or not to be,” then you've succeeded in writing a genetic algorithm.
Create a sketch that generates random strings. You'll need to know how to do this in order to implement the genetic algorithm example that will shortly follow. How long does it take for p5.js to randomly generate the string “cat”? How might you adapt this to generate a random design using p5.js’s shape-drawing functions?
Before I begin walking through the genetic algorithm, I want to take a moment to describe three core principles of Darwinian evolution that will be required for the simulation. In order for natural selection to occur as it does in nature, all three of these elements must be present. Note I’ll be using the generic term “creature” to describer any given element of a population and “parent/child” to refer to the generational relationship between creatures.
Next I’d like to walk through the narrative of the genetic algorithm. I'll do this in the context of the typing monkey. The algorithm itself will be divided into two parts: a set of conditions for initialization—setup()—and the steps that are repeated over and over again—draw()— until the correct phrase is found.
In the context of the typing monkey example, the first step is to create a population of phrases. (Note that I am using the term “phrase” rather loosely, this is the “creature” for this example, but isn’t very “creature”-like as it refers to a string of characters.) This begs the question: How to create this population? Here is where the Darwinian principle of variation applies. Let’s say for the sake of simplicity, that I am trying to evolve the phrase “cat” and that I have a population of three phrases.
| rid |
| won |
| hug |
Sure, there is variety in the three phrases above, but try to mix and match the characters every which way and you will never get cat. There is not enough variety here to evolve the optimal solution. However, if there were a population of thousands of phrases, all generated randomly, chances are that at least one phrase would have a c as the first character, one will have an a as the second, and one a t as the third. A large population will most likely provide enough variety to generate the desired phrase (and in Part 2 of the algorithm, I'll demonstrate another mechanism to introduce more variation in case there isn’t enough in the first place). Step 1 can therefore be descrived as follows:
Create a population of randomly generated elements.
Element is perhaps a better, more general purpose term than creature. But what is the element itself? As you move through the examples in this chapter, you'll see several different scenarios; you might have a population of images or a population of vehicles à la Chapter 6. The part that is new for you in this chapter, is that each element, each member of that population, has a virtual “DNA.” Its DNA is a set of properties (you could also call them “genes”) that describe how a given element looks or behaves. In the case of the typing monkey, for example, the DNA could be a string of characters.
In the field of genetics, there is an important distinction between the concepts genotype and phenotype. The actual genetic code—in our case, the digital information itself—is an element’s genotype. This is what gets passed down from generation to generation. The phenotype, however, is the expression of that data. This distinction is key to how you will use genetic algorithms in your own work. What are the objects in your world? How will you design the genotype for your objects (the data structure to store each object’s properties) as well as the phenotype (what are you using these variables to express?) We do this all the time in graphics programming. The simplest example is probably color.
| Genotype | Phenotype |
|---|---|
| 0 | |
| 127 | |
| 255 |
Think of the genotype as the digital information, the data that represents color, in the case of grayscale values an integer between 0 and 255 . How you choose to express the data is arbitrary: a red value, a green value, and a blue value. In a different approach, you could use the values to describe the length of a line, the weight of a force, and so on.
| Same Genotype | Different Phenotype (line length) |
|---|---|
| 0 | |
| 127 | |
| 255 |
The nice thing about the monkey-typing example is that there is no difference between genotype and phenotype. The DNA data itself is a string of characters and the expression of that data is that very string.
So, I can finally end the discussion of this first step and be even more specific with its description, saying:
Create a population of N elements, each with randomly generated DNA.
Here is where the Darwinian principle of selection is applied by evaluating the population and determining which members are “fit” to be selected as parents for the next generation. The process of selection can be divided into two steps.
For the genetic algorithm to function properly, I will need to design what is referred to as a fitness function. The function will produce a numeric score to describe the fitness of a given element of the population. This, of course, is not how the real world works at all. Creatures are not given a score; rather they survive or do not survive. But in the case of a traditional genetic algorithm, where the goal is to evolve an optimal solution to a problem, a mechanism to numerically evaluate any given possible solution is required.
Let’s examine the current scenario, the typing monkey. Again, let’s simplify and assign the target phrase: “cat”. Assume three members of the population: hut, car, and box. Car is obviously the most fit, given that it has two correct characters, hut has only one, and box has zero. And there it is, a fitness function:
| DNA | Fitness |
|---|---|
| car | 2 |
| hut | 1 |
| box | 0 |
I will eventually want to look at examples with more sophisticated fitness functions, but this is a good place to start.
Once the fitness has been calculated for all members of the population, the next step is to select which members are fit to become parents and place them in a mating pool. There are several different approaches for this step. For example, I could employ what is known as the elitist method and say, “Which two members of the population scored the highest? You two will make all the children for the next generation.” This is probably one of the easier methods to code; however, it flies in the face of the principle of variation. If two members of the population (out of perhaps thousands) are the only ones available to reproduce, the next generation will have little variety and this may stunt the evolutionary process. I could instead make a mating pool out of a larger number—for example, the top 50% of the population. This is also easy to code, but it will not produce optimal results. In this case, the highest-scoring elements would have the same chance of being selected as the ones toward the middle. In the case of 1,000 phrases why should the phrase ranked 500th have a solid shot of reproducing, while phrase 501 has no shot?
A better solution for the mating pool is to use a probabilistic method, which I’ll call the “wheel of fortune” (also known as the “roulette wheel”). To illustrate this method, let’s consider a scenario where there is a population of five elements, each with a fitness score.
| Element | Fitness |
|---|---|
| A | 3 |
| B | 4 |
| C | 0.5 |
| D | 1 |
| E | 1.5 |
The first step is to normalize all the scores. Remember normalizing a vector? That involved taking a vector and standardizing its length, setting it to 1. Normalizing a set of fitness scores can be accomplished by standardizing their range to between 0 and 1, as a percentage of total fitness. Let’s add up all the fitness scores.
The next step is to divide each score by the total fitness, resulting in the normalized fitness.
| Element | Fitness | Normalized Fitness | Expressed as a Percentage |
|---|---|---|---|
| A | 3 | 0.3 | 30% |
| B | 4 | 0.4 | 40% |
| C | 0.5 | 0.05 | 5% |
| D | 1 | 0.1 | 10% |
| E | 1.5 | 0.1 | 15% |
Now it’s time for the wheel of fortune.
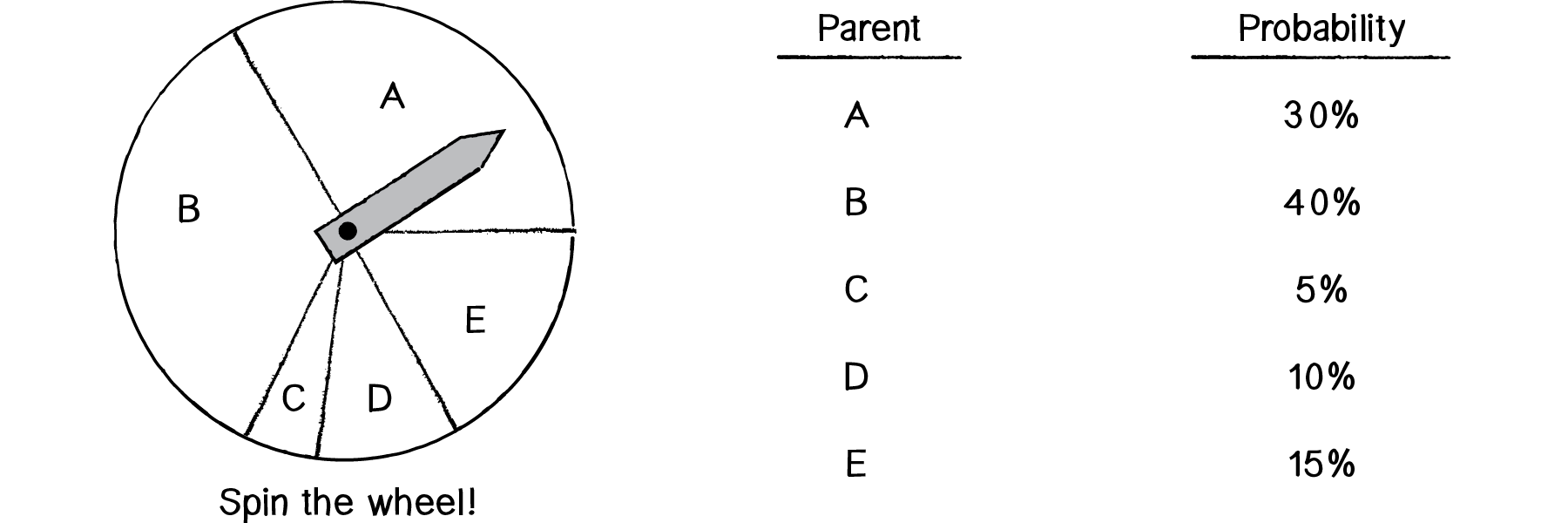
Spin the wheel and you’ll notice that Element B has the highest chance of being selected, followed by A, then E, then D, and finally C. This probability-based selection according to fitness is an excellent approach. One, it guarantees that the highest-scoring elements will be most likely to reproduce. Two, it does not entirely eliminate any variation from the population. Unlike with the elitist method, even the lowest-scoring element (in this case C) has a chance to pass its information down to the next generation. It’s quite possible (and often the case) that even low-scoring elements have a tiny nugget of genetic code that is truly useful and should not entirely be eliminated from the population. For example, in the case of evolving “to be or not to be”, we might have the following elements.
| A | "to be or not to go" |
| B | "to be or not to pi" |
| C | "xxxxxxxxxxxxxxxxbe" |
As you can see, elements A and B are clearly the most fit and would have the highest score. But neither contains the correct characters for the end of the phrase. Element C, even though it would receive a very low score, happens to have the genetic data for the end of the phrase. And so while I might want A and B to be picked to generate the majority of the next generation, I would still want C to have a small chance to participate in the reproductive process.
Now that I’ve demonstrated a strategy for picking parents, I need to examine how to use reproduction to create the population’s next generation, keeping in mind the Darwinian principle of heredity—that children inherit properties from their parents. Again, there are a number of different techniques that could be employed here. For example, one reasonable (and easy to program) strategy is “cloning”, meaning just one parent is picked and an exact copy of that parent is created as a child element. The standard approach with genetic algorithms, however, is to pick two parents and create a child according to the following steps.
1) Crossover.
Crossover involves creating a child out of the genetic code of two parents. In the case of the monkey-typing example, let’s assume that two phrases from the mating pool have been picked (as outlined in the selection step). I’ll simplify and use strings of length 6 (instead of the 18 required for “to be or not to be”.)
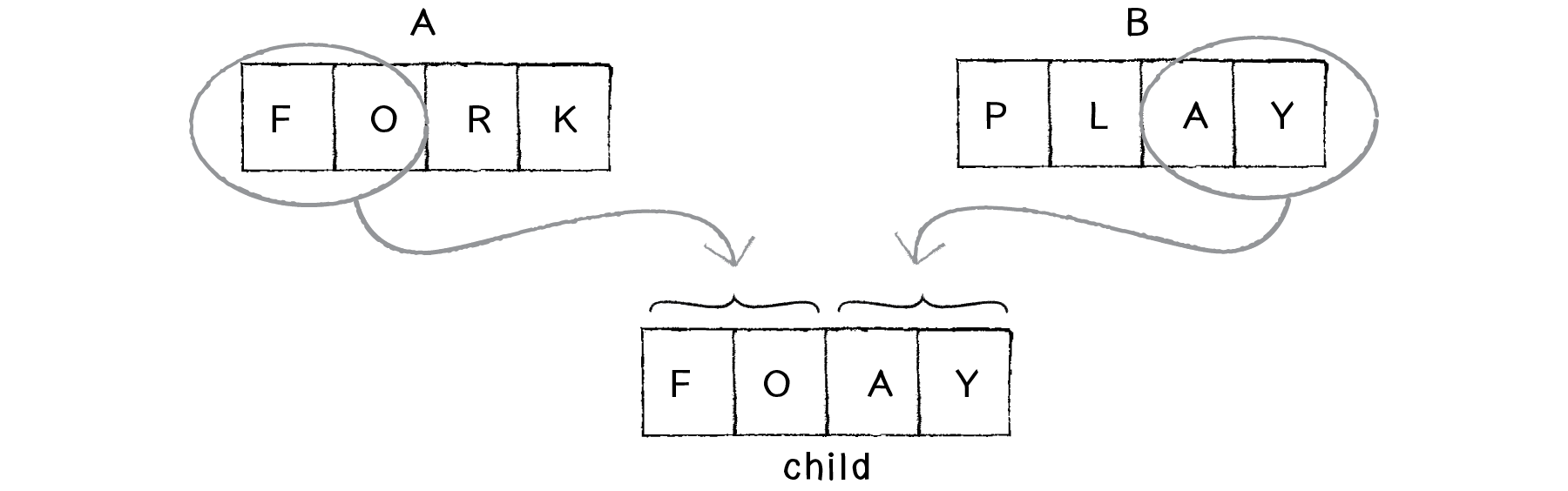
| Parent A | “coding” |
| Parent B | “nature” |
The task at hand is now to create a child phrase from these two. Perhaps the most obvious way (let’s call this the “50/50 method”) would be to take the first three characters from A and the second three from B, leaving:
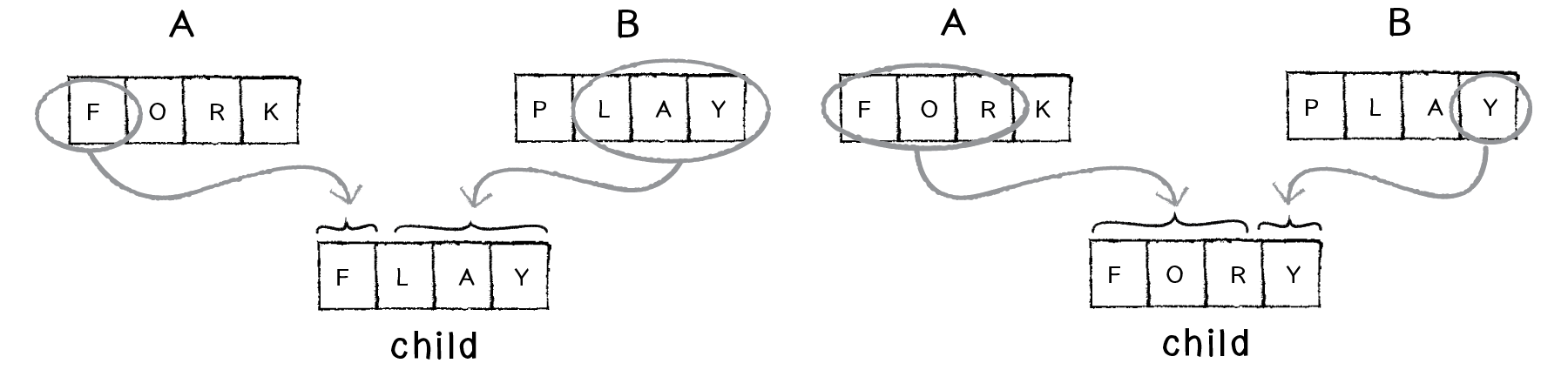
A variation of this technique is to pick a random midpoint. In other words, I don’t have to pick exactly half of the characters from each parent. I could use a combination of 1 and 5 or 2 and 4. This is preferable to the 50/50 approach, since the variety of possibilities is increased for for the next generation.
Another possibility is to randomly select a parent for each character in the child string. You can think of this as flipping a coin six times: heads take from parent A, tails from parent B. Here there are even more possible outcomes: “codurg”, “natine”, “notune”, "cadune”, etc.
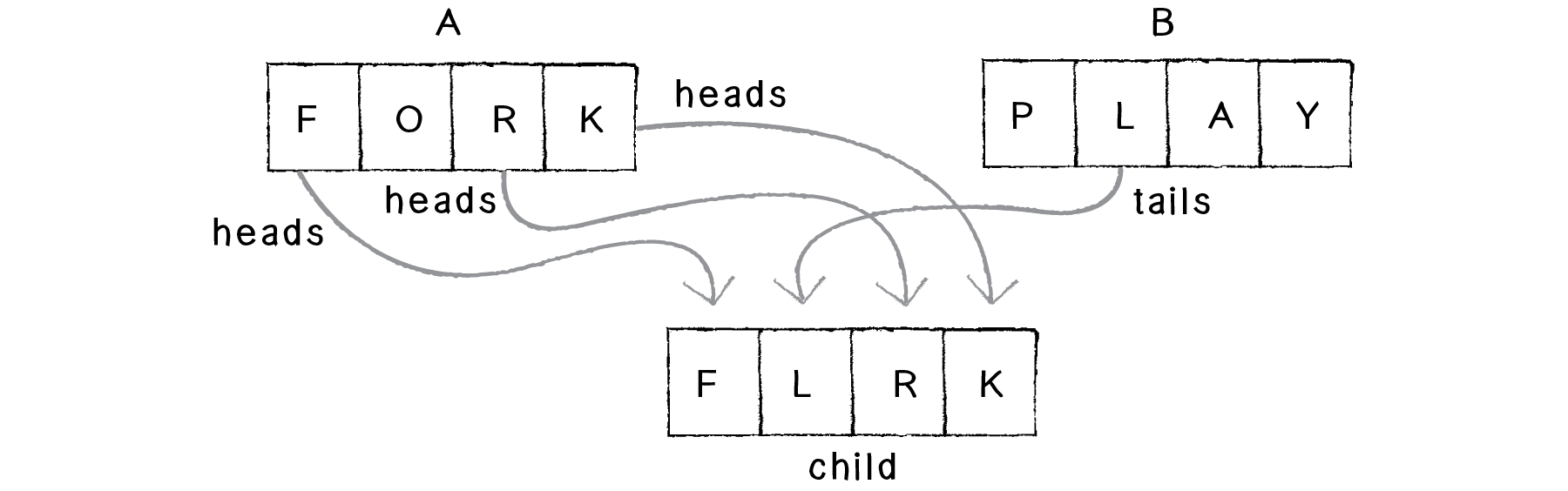
This strategy will not significantly change the outcome from the random midpoint method; however, if the order of the genetic information plays some role in expressing the phenotype, you may prefer one solution over the other.
2) Mutation.
Once the child DNA has been created via crossover, one final process is applied before adding the child to the next generation: mutation. While mutation is optional and unnecessary in some cases, it exists to further uphold the Darwinian principle of variation. The initial population was created randomly, ensuring that there is some variety of elements. However, this variation is limited by the size of the population, and mutation introduces additional variety throughout the evolutionary process.
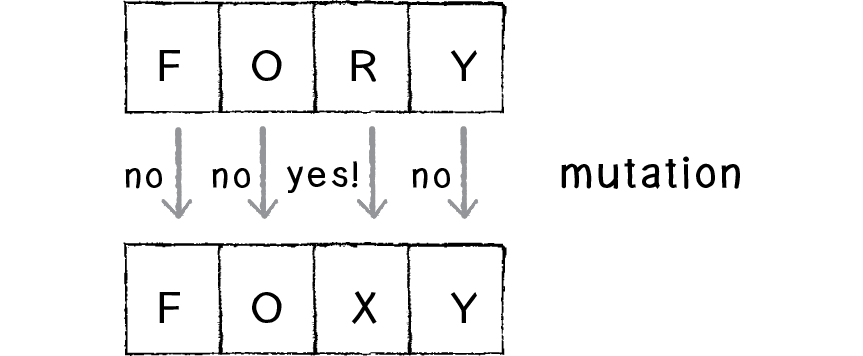
Mutation is described in terms of a rate. A given genetic algorithm might have a mutation rate of 5% or 1% or 0.1%, etc. Let’s start with the string “nature”. If the mutation rate is 1%, this means that for each character in the phrase “nature”, there is a 1% chance that it will mutate. What does it mean for a character to mutate? In this case, mutation could be defined as picking a new random character. A 1% probability is fairly low, and most of the time mutation will not occur at all in a six-character string (~94% of the time to be more precise). However, when it does, the mutated character is replaced with a randomly generated one (see Figure 9.6).
As you’ll see in the examples, the mutation rate can greatly affect the behavior of the system. A very high mutation rate (such as, say, 80%) would negate the entire evolutionary process and leave you with something more akin to a brute force algorithm itself. If the majority of a child’s genes are generated randomly, then you cannot guarantee that the more “fit” genes occur with greater frequency with each successive generation.
The process of selection (picking two parents) and reproduction (crossover and mutation) is applied over and over again N times until there is a new population of N elements. At this point, the new population of children becomes the current population and the process loops back to evaluating fitness, then selection, and finally reproduction once again.
Now that I have described all the steps of the genetic algorithm in detail, it’s time to translate these steps into code. Because the description here was a bit longwinded, let’s revisit the algorithm with an outlined overview first. I’ll then cover each of the three steps in its own section, working out the code.
SETUP:
Step 1: Initialize. Create a population of N elements, each with randomly generated DNA.
LOOP:
Step 2: Selection. Evaluate the fitness of each element of the population and build a mating pool.
Step 3: Reproduction. Repeat N times:
Step 4. Replace the old population with the new population and return to Step 2.
If I'm going to create a population, I need a data structure to store a list of elements in the population.
// An array for the population of ele let population = [];
Choosing an array for a list is straightforward, but the question remains: an array of what? An object is an excellent choice for storing the genetic information, as it can hold multiple properties and methods. These “genetic” objects will be structured according to a class that I will call DNA.
class DNA {
}
What should go in the DNA class? For a typing monkey, its DNA would be the random phrase it types, a string of characters. However, using an array of characters (rather than a string object) provides a more generic template that can extend easily to other data types. For example, the DNA of a creature in a physics system could be an array of vectors—or for an image, an array of numbers (RGB pixel values). Any set of properties can be listed in an array, and even though a string is convenient for this particular scenario, an array will serve as a better foundation for future evolutionary examples.
The genetic algorithm specifies that I create a population of N elements, each with randomly generated genes. The DNA constructor therefore includes a loop to fill in each element of the genes array.
class DNA {
constructor(length){
//{!1} The individual "genes" are stored in an array
this.genes = [];
// There are "length" genes
for (let i = 0; i < length; i++) {
// Each gene is a random character
this.genes[i] = randomCharacter();
}
}
}
In order to randomly generate a character, I will write a helper function called randomCharacter() for each individual gene.
// Return a random character (letter, number, symbol, space, etc)
function randomCharacter() {
let c = floor(random(32, 127));
return String.fromCharCode(c);
}
The random numbers picked correspond to a specific character according to a standard known as ASCII (American Standard Code for Information Interchange). String.fromCharCode(c) is a native JavaScript function that converts the number into its corresponding character based on that standard. Note that this function will also return numbers, punctuation marks, and special characters. A more modern approach might involve the “Unicode” standard, which includes emojis and characters from a wide variety of world languages.
Now that I have the constructor, I can return to setup() and initialize each DNA object in the population array.
let population = [];
function setup() {
for (let i = 0; i < population.length; i++) {
//{!1} Initializing each element of the population, 18 is hardcoded for now as the length of the genes array.
population[i] = new DNA(18);
}
}
The DNA class is not at all complete. I'll need to add functions to it to perform all the other tasks in the genetic algorithm, which I'll do as I walk through steps 2 and 3.
Step 2 reads, “Evaluate the fitness of each element of the population and build a mating pool.” I'll start by evaluating each object’s fitness. Earlier I stated that one possible fitness function for the typed phrases is the total number of correct characters. I will revise this fitness function a little bit and state it as the percentage of correct characters—i.e., the total number of correct characters divided by the total characters.
Where should I calculate the fitness? Since the DNA class contains the genetic information (the phrase I will test against the target phrase), I can write a function inside the DNA class itself to score its own fitness. Let’s assume a target phrase:
let target = "to be or not to be";
We can now compare each “gene” against the corresponding character in the target phrase, incrementing a counter each time we get a correct character.
class DNA {
constructor(length) {
this.genes = [];
//{!1} Adding a variable to track fitness.
this.fitness = 0;
for (let i = 0; i < length; i++) {
this.genes[i] = randomCharacter();
}
}
// Compute fitness as % of "correct" characters
calculateFitness(target) {
let score = 0;
for (let i = 0; i < this.genes.length; i++) {
if (this.genes[i] == target.charAt(i)) {
score++;
}
}
this.fitness = score / target.length;
}
}
Since fitness is calculated for each subsequent generation, the very first step I'll take is to call the fitness function for each member of the population inside the draw() loop.
function draw() {
for (let i = 0; i < population.length; i++) {
population[i].calculateFitness();
}
}
Once the fitness scores have been computed, the next step is to move onto the "mating pool" for the reproduction process. The mating pool is a data structure from which two parents are repeatedly selected. Recalling the description of the selection process, the goal is to pick parents with probabilities calculated according to fitness. In other words, the members of the population with the highest fitness scores should be most likely to be selected; those with the lowest scores, the least likely.
In the Introduction, I covered the basics of probability and generating a custom distribution of random numbers. I'm going to use the same techniques here to assign a probability to each member of the population, picking parents by spinning the “wheel of fortune.” Revisiting Figure 9.2 again, your mind might immediately go back to chapter 3 and contemplate coding a simulation of an actual spinning wheel. As fun as this might be (and you should make one!) it’s quite unnecessary.
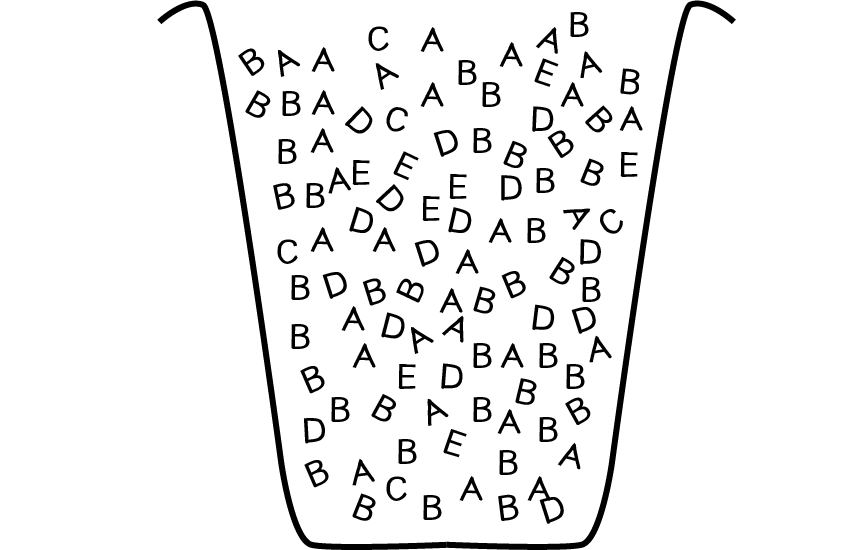
One solution that could work here is to pick from the five options depicted in Figure 9.2 (ABCDE) according to their probabilities by filling an array with multiple instances of each parent. In other words, let’s say you had a bucket of wooden letters—30 As, 40 Bs, 5 Cs, 10 Ds, and 15 Es.
If you were to pick a random letter out of that bucket, there’s a 30% chance you’ll get an A, a 5% chance you’ll get a C, and so on. For the genetic algorithm code, that bucket could be an array and each wooden letter a potential parent DNA object. The mating pool is therefore created by adding each parent to the array a number of times scaled according to its fitness score.
//{!1} Start with an empty mating pool.
let matingPool = [];
for (let i = 0; i < population.length; i++) {
//{!1} n is equal to fitness times 100,
// 100 is an arbitrary way to scale the % fitness to a larger integer value
let n = floor(population[i].fitness * 100);
for (let j = 0; j < n; j++) {
//{!1} Add each member of the population to the mating pool n times.
matingPool.push(population[i]);
}
}
With the mating pool ready to go, it’s time to select two parents! Again, it’s somewhat of an arbitrary decision to pick two. It certainly mirrors human reproduction and is the standard means in the textbook genetic algorithm, but in terms of creative applications, there really aren’t restrictions here. You could choose only one parent for “cloning,” or devise a reproduction methodology for picking three or four parents from which to generate child DNA. For the demonstration here, I'll stick to two parents and call them parentA and parentB.
First thing I need are two random indices into the mating pool—random numbers between 0 and the size of the array.
let aIndex = floor(random(matingPool.length); let bindex = floor(random(matingPool.length);
I can then use the indices to retrieve a DNA instance from the mating pool array.
let parentA = matingPool[aIndex]; let parentB = matingPool[bIndex];
Let's take a moment here to revisit the discussion on non-uniform distributions of random numbers from the Introduction chapter. There I implemented the "accept-reject" method. If applied here, the approach would be to pick a single element from the original population array and then a second, qualifying random number to check against the fitness value.
However, there's another excellent alternative worth exploring that also capitalizes on the principle of fitness proportionate selection.
To understand how this works, let’s consider a relay race where each member of the population runs a given distance tied to their fitness. The higher the fitness, the farther they run. Let’s also assume that the fitness values have been normalized to all add up to 1 (just like with the “wheel of fortune.”). The first step is to pick a starting line—a random distance from the finish. This distance is a random number between 0 and 1 (and you’ll see in a moment that the finish line is assumed to be at 0.)
let start = random(1);
Then the race begins with first member of the population at the starting line.
let index = 0;
The runner travels a distance defined by its normalized fitness score and hands the baton to the next runner.
while (start > 0) {
// Move a distance according to fitness
start = start - population[index].fitness;
// Next element
index++;
}
The steps are repeated over and over again in a while loop until the race ends (start is less than or equal to 0, the “finish” line). Once a runner crosses that finish threshold, it is selected as a parent. Let’s put it all together in a function which returns the selected element.
function weightedSelection() {
// Start with the first element
let index = 0;
// Pick a starting point
let start = random(1);
// At the finish line?
while (start > 0) {
// Move a distance according to fitness
start = start - population[index].fitness;
// Next element
index++;
}
// Undo moving to the next element since the finish has been reached
index--;
return population[index];
}
This works well for selection as each and every member has a shot at crossing the finish but those who run longer distances (e.g. those with higher fitness scores) have a better chance of making it there. A significant advantage of this method is memory efficiency—it doesn't require an additional array full of multiple references to each element. However, just like “accept-reject” algorithm, this approach can be computationally more demanding, especially for large populations, as it requires iterating through the population for each selection. The mating pool method only needs a single lookup.
Depending on the specific requirements and constraints of your application of genetic algorithms, one approach might prove more suitable than the other. I’ll alternate between them in the examples outlined in this chapter.
Revisit the accept-reject algorithm from the introduction. Rewrite the weightedSelection() function to use accept-reject instead.
In some cases, the wheel of fortune algorithm will have an extraordinarily high preference for some elements over others. Take the following probabilities:
| Element | Probability |
|---|---|
| A | 98% |
| B | 1% |
| C | 1% |
This is sometimes undesirable given how it will decrease the amount of variety in this system. A solution to this problem is to replace the calculated fitness scores with the ordinals of scoring (meaning their rank).
| Element | Rank | Probability |
|---|---|---|
| A | 1 | 50% (1/2) |
| B | 2 | 33% (1/3) |
| C | 3 | 17% (1/6) |
Rewrite the mating pool algorithm to use this method instead.
For any of these algorithms, it’s possible that the same parent could be picked twice. If I wanted to exclude this possibility, I could enhance the algorithm to ensure that this is not possible. This would likely have very little impact on the end result, but it may be worth exploring as an exercise.
Pick any of the weighted selection algorithms and adapt the algorithm to guarantee that two unique “parents” are picked.
Once I have the two parents, the next step is to perform a crossover operation to generate child DNA, followed by mutation.
// A function for crossover let child = parentA.crossover(parentB); // A function for mutation child.mutate();
Of course, the functions crossover() and mutate() don’t magically exist in the DNA class; I will have to write them. The way crossover() is called above indicates that the function should receive an instance of DNA as an argument (parentB) and returns a new instance of DNA, the child.
crossover(partner) {
// The child is a new instance of DNA.
// (Note that the genes are generated randomly in DNA constructor,
// but the crossover function will override the array.)
let child = new DNA(this.genes.length);
//{!1} Picking a random “midpoint” in the genes array
let midpoint = floor(random(this.genes.length));
for (let i = 0; i < this.genes.length; i++) {
// Before the midpoint genes from this DNA
if (i < midpoint) {
child.genes[i] = this.genes[i];
// After the midpoint from the partner DNA
} else {
child.genes[i] = partner.genes[i];
}
}
return child;
}
The above implementation uses the “random midpoint” method of crossover, in which the first section of genes is taken from parent A and the second from parent B.
Rewrite the crossover function to use the “coin flipping” method instead, in which each gene has a 50% chance of coming from parent A and a 50% chance of coming from parent B.
The mutate() function is even simpler to write than crossover(). All I need to do is loop through the array of genes and randomly pick a new character according to the defined mutation rate. With a mutation rate of 1%, for example, a new character would only be generated one out of a hundred times.
let mutationRate = 0.01;
if (random(1) < mutationRate) {
// Any code here would be executed 1% of the time.
}
The entire function therefore reads:
mutate(mutationRate) {
//{!1} Looking at each gene in the array
for (let i = 0; i < this.genes.length; i++) {
//{!1} Check a random number against mutation rate
if (random(1) < mutationRate) {
//{!1} Mutation, a new random character
this.genes[i] = randomCharacter();
}
}
}
You may have noticed that I've walked through the steps of the genetic algorithm twice, once describing it in narrative form and another time with code snippets implementing each of the steps. What I’d like to do in this section is condense the previous two sections into one page, with the algorithm described in just three steps and the corresponding code alongside.

// [TBD] Global variables needed for the GA
// Mutation rate
let mutationRate = 0.01;
// Population Size
let populationSize = 150;
// Population array
let population = [];
// Target phrase
let target = "to be or not to be";
function setup() {
createCanvas(640, 360);
//{!3} Step 1: Initialize Population
for (let i = 0; i < populationSize; i++) {
population[i] = new DNA(target.length);
}
}
function draw() {
// Step 2: Selection
//{!3} Step 2a: Calculate fitness.
for (let i = 0; i < population.length; i++) {
population[i].calculateFitness(target);
}
// Step 2b: Build mating pool.
let matingPool = [];
for (let i = 0; i < population.length; i++) {
//{!4} Add each member n times according to its fitness score.
let n = floor(population[i].fitness * 100);
for (let j = 0; j < n; j++) {
matingPool.push(population[i]);
}
}
// Step 3: Reproduction
for (let i = 0; i < population.length; i++) {
let aIndex = floor(random(matingPool.length));
let bIndex = floor(random(matingPool.length));
let partnerA = matingPool[aIndex];
let partnerB = matingPool[bIndex];
// Step 3a: Crossover
let child = partnerA.crossover(partnerB);
// Step 3b: Mutation
child.mutate(mutationRate);
//{!1} Note that we are overwriting the population with the new
// children. When draw() loops, we will perform all the same
// steps with the new population of children.
population[i] = child;
}
}
The sketch.js file precisely mirrors the steps of the genetic algorithm. However, most of the functionality called upon is actually present in the DNA class itself.
class DNA {
//{.code-wide} Constructor (makes a random DNA)
constructor(length) {
this.genes = [];
this.fitness = 0;
for (let i = 0; i < length; i++) {
this.genes[i] = randomCharacter();
}
}
//{.code-wide} Converts array to String—PHENOTYPE.
getPhrase() {
return this.genes.join("");
}
//{.code-wide} Calculate fitness.
calculateFitness(target) {
let score = 0;
for (let i = 0; i < this.genes.length; i++) {
if (this.genes[i] == target.charAt(i)) {
score++;
}
}
this.fitness = score / target.length;
}
//{.code-wide} Crossover
crossover(partner) {
let child = new DNA(this.genes.length);
let midpoint = floor(random(this.genes.length));
for (let i = 0; i < this.genes.length; i++) {
if (i < midpoint) {
child.genes[i] = this.genes[i];
} else {
child.genes[i] = partner.genes[i];
}
}
return child;
}
//{!7 .code-wide} Mutation
mutate(mutationRate) {
for (let i = 0; i < this.genes.length; i++) {
if (random(1) < mutationRate) {
this.genes[i] = randomCharacter();
}
}
}
}
// Return a random character (letter, number, symbol, space, etc)
function randomCharacter() {
let c = floor(random(32, 127));
return String.fromCharCode(c);
}
Add features to the above example to report more information about the progress of the genetic algorithm itself. For example, show the phrase closest to the target each generation, as well as report on the number of generations, average fitness, etc. Stop the genetic algorithm once it has solved the phrase. Consider writing a Population class to manage the GA, instead of including all the code in draw().
The nice thing about using genetic algorithms in a project is that example code can easily be ported from application to application. The core mechanics of selection and reproduction don’t need to change. There are, however, three key components to genetic algorithms that you, the developer, will have to customize for each use. This is crucial to moving beyond trivial demonstrations of evolutionary simulations (as in the Shakespeare example) to creative uses in projects that you make in p5.js and other creative programming environments.
There aren’t a lot of variables to the genetic algorithm itself. In fact, if you look at the previous example’s code, you’ll see only two global variables (not including the arrays to store the population and mating pool).
let mutationRate = 0.01; let populationSize = 150;
These two variables can greatly affect the behavior of the system, and it’s not such a good idea to arbitrarily assign them values (though tweaking them through trial and error is a perfectly reasonable way to arrive at optimal values).
The values I chose for the Shakespeare demonstration were picked to virtually guarantee that the genetic algorithm would solve for the phrase, but not too quickly (approximately 1,000 generations on average) so as to demonstrate the process over a reasonable period of time. A much larger population, however, would yield faster results (if the goal were algorithmic efficiency rather than demonstration). Here is a table of some results.
| Population Size | Mutation Rate | Number of Generations until Phrase Solved | Total Time (in seconds) until Phrase Solved |
|---|---|---|---|
| 150 | 1% | 1,089 | 18.8 |
| 300 | 1% | 448 | 8.2 |
| 1,000 | 1% | 71 | 1.8 |
| 50,000 | 1% | 27 | 4.3 |
Notice how increasing the population size drastically reduces the number of generations needed to solve for the phrase. However, it doesn’t necessarily reduce the amount of time. Once the population balloons to fifty thousand elements, the sketch begins to run slowly, given the amount of time required to process fitness and build a mating pool out of so many elements. (There are, of course, optimizations that could be made should you require such a large population.)
In addition to the population size, the mutation rate can greatly affect performance.
| Population Size | Mutation Rate | Number of Generations until Phrase Solved | Total Time (in seconds) until Phrase Solved |
|---|---|---|---|
| 1,000 | 0% | 37 or never? | 1.2 or never? |
| 1,000 | 1% | 71 | 1.8 |
| 1,000 | 2% | 60 | 1.6 |
| 1,000 | 10% | never? | never? |
Without any mutation at all (0%), you just have to get lucky. If all the correct characters are present somewhere in an element of the initial population, you’ll evolve the phrase very quickly. If not, there is no way for the sketch to ever reach the exact phrase. Run it a few times and you’ll see both instances. In addition, once the mutation rate gets high enough (10%, for example), there is so much randomness involved (1 out of every 10 letters is random in each new child) that the simulation is pretty much back to a random typing monkey. In theory, it will eventually solve the phrase, but you may be waiting much, much longer than is reasonable.
Playing around with the mutation rate or population size is pretty easy and involves little more than typing numbers in your sketch. The real hard work of a developing a genetic algorithm is in writing a fitness function. If you cannot define your problem’s goals and evaluate numerically how well those goals have been achieved, then you will not have successful evolution in your simulation.
Before I move onto other scenarios exploring more sophisticated fitness functions, I want to look at flaws in my Shakespearean fitness function. Consider solving for a phrase that is not nineteen characters long, but one thousand. Now, take two elements of the population, one with 800 characters correct and one with 801. Here are their fitness scores:
| Phrase | Characters Correct | Fitness |
|---|---|---|
| A | 800 | 80.0% |
| B | 801 | 80.1% |
There are a couple of problems here. First, I am adding elements to the mating pool N numbers of times, where N equals fitness multiplied by 100. Objects can only be added to an array a whole number of times, and so A and B will both be added 80 times, giving them an equal probability of being selected. Even with an improved solution that takes floating point probabilities into account, 80.1% is only a teeny tiny bit higher than 80%. But getting 801 characters right is a whole lot better than 800 in the evolutionary scenario. I really want to make that additional character count. I want the fitness score for 801 characters to be substantially better than the score for 800.
To put it another way, here's a graph the fitness function.

This is a linear graph; as the number of characters goes up, so does the fitness score. However, what if the fitness increased at an accelerating rate as the number of correct characters increased?

The more correct characters, the even greater the fitness. I can achieve this type of result in a number of different ways. For example, I could say:
Here, the fitness scores increase quadratically, meaning proportional to the square of the number of correct characters. Let’s say I have two members of the population, one with five correct characters and one with six. The number 6 is a 20% increase over the number 5. However, by squaring the correct characters, the fitness value has increased to 36 from 25, a 44% increase.
| correct characters | fitness |
|---|---|
| 5 | 25 |
| 6 | 36 |
Here’s another formula.
| correct characters | fitness |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
Here, the fitness scores increase exponentially, doubling with each additional correct character.
Rewrite the fitness function to increase quadratically or exponentially according to the number of correct characters. Note that you will likely have to normalize the fitness values to a range between 0 and 1 so they can be added to the mating pool a reasonable number of times or use a different “weighted selection” method.
While this rather specific discussion of exponential vs. linear fitness functions is an important detail in the design of a good fitness function, I don’t want you to miss the more important point here: Design your own fitness function! I seriously doubt that any project you undertake in p5.js with genetic algorithms will actually involve counting the correct number of characters in a string. In the context of this book, it’s more likely you will be looking to evolve a creature that is part of a physics system. Perhaps you are looking to optimize the weights of steering behaviors so a creature can best escape a predator or avoid an obstacle or make it through a maze. You have to ask yourself what you’re hoping to evaluate.
Let’s consider a racing simulation in which a vehicle is evolving a design optimized for speed.
How about a mouse that is evolving the optimal way to fine a piece of cheese?
The design of computer-controlled players in a game is also a common scenario. Let’s say you are programming a soccer game in which the user is the goalie. The rest of the players are controlled by your program and have a set of parameters that determine how they kick a ball towards the goal. What would the fitness score for any given player be?
This, of course, is a simplistic take on the game of soccer, but it illustrates the point. The more goals a player scores, the higher its fitness, and the more likely its genetic information will appear in the next game. Even with a fitness function as simple as the one described here, this scenario is demonstrating something very powerful—the adaptability of a system. If the players continue to evolve from game to game to game, when a new human user enters the game with a completely different strategy, the system will quickly discover that the fitness scores are going down and evolve a new optimal strategy. It will adapt. (Don’t worry, there is very little danger in this resulting in sentient robots that will enslave all humans.)
In the end, if you do not have a fitness function that effectively evaluates the performance of the individual elements of your population, you will not have any evolution. And the fitness function from one example will likely not apply to a totally different project. So this is the part where you get to shine. You have to design a function, sometimes from scratch, that works for your particular project. And where do you do this? All you have to edit are those few lines of code inside the function that computes the fitness variable.
calculateFitness() {
????????????
????????????
this.fitness = ??????????
}
The final key to designing your own genetic algorithm relates to how you choose to encode the properties of your system. What are you trying to express, and how can you translate that expression into a bunch of numbers? What is the genotype and phenotype?
When talking about the fitness function, I happily assumed I could create computer-controlled kickers that each had a “set of parameters that determine how they kick a ball towards the goal.” However, what those parameters are and how you choose to encode them is up to you.
I started with the Shakespeare example because of how easy it was to design both the genotype (an array of characters) and its expression, the phenotype (the string displayed on the canvas).
The good news is—and I hinted at this at the start of this chapter—you’ve really been doing this all along. Anytime you write a class in p5.js, you make a whole bunch of variables.
class Vehicle {
constructor(){
this.maxspeed = ????;
this.maxforce = ????;
this.size = ????;
this.separationWeight = ????;
{inline}// and more...
}
All you need to do to evolve those parameters is to turn them into an array, so that the array can be used with all of the functions—crossover(), mutate(), etc.—found in the DNA class. One common solution is to use an array of floating point numbers between 0 and 1.
class DNA {
constructor(length) {
// An empty array
this.genes = [];
for (let i = 0; i < length; i++) {
// Always pick a number between 0 and 1.
this.genes[i] = random(1);
}
}
}
Notice how I've now put the genetic data (genotype) and its expression (phenotype) into two separate classes. The DNA class is the genotype and the Vehicle class is the expression of those behaviors animating that data visually—it is the phenotype. The two can be linked by including a DNA instance inside the Vehicle class itself.
class Vehicle {
constructor() {
//{!1} A DNA object embedded into the Vehicle class
this.dna = new DNA(4);
//{!4} Using the genes to set variables
this.maxspeed = dna.genes[0];
this.maxforce = dna.genes[1];
this.size = dna.genes[2];
this.separationWeight = dna.genes[3];
//{!1} Etc.
}
Of course, you most likely don’t want all your variables to have a range between 0 and 1. But rather than try to remember how to adjust those ranges in the DNA class itself, it’s easier to pull the genetic information from the DNA object and use p5.js’s map() function to change the range. For example, if you want a size variable between 10 and 72, you would say:
this.size = map(this.dna.genes[2], 0, 1, 10, 72);
In other cases, you may want to design a genotype that is an array of objects. Consider the design of a rocket with a series of “thruster” engines. You could consider each thruster to be a vector that describes its direction and relative strength.
class DNA {
constructor(length) {
// The genotype is an array of vectors.
this.genes = [];
for (let i = 0; i < length; i++) {
//{!1} A PVector pointing in a random direction
this.genes[i] = p5.Vector.random2D();
//{!1} And scaled randomly
this.genes[i].mult(random(10));
}
}
}
The phenotype would be a Rocket class that participates in a physics system.
class Rocket {
constructor(){
this.dna = ????;
[inline]// etc.
}
}
What’s great about this technique of dividing the genotype and phenotype into separate classes (DNA and Rocket for example) is that when it comes time to build all of the code, you’ll notice that the DNA class I developed earlier remains intact. The only thing that changes is the kind of data stored in the array (number, vector, etc.) and the expression of that data in the phenotype class.
In the next section, I'll follow this idea a bit further and walk through the necessary steps for an example that involves moving bodies and an array of vectors as DNA.
I picked the rocket idea for a specific reason. In 2009, Jer Thorp released a genetic algorithms example on his blog entitled “Smart Rockets.” Jer points out that NASA uses evolutionary computing techniques to solve all sorts of problems, from satellite antenna design to rocket firing patterns. This inspired him to create a Flash demonstration of evolving rockets. Here is a description of the scenario:
A population of rockets launches from the bottom of the screen with the goal of hitting a target at the top of the screen (with obstacles blocking a straight line path).
Each rocket is equipped with five thrusters of variable strength and direction. The thrusters don’t fire all at once and continuously; rather, they fire one at a time in a custom sequence.
In this section, I'm going to evolve my own simplified Smart Rockets, inspired by Jer Thorp’s. When I get to the end of the section, I'll leave implementing some of Jer’s additional advanced features as an exercise.
My rockets will have only one thruster, and this thruster will be able to fire in any direction with any strength for every frame of animation. This isn’t particularly realistic, but it will make building out the example a little easier. (You can always make the rocket and its thrusters more advanced and realistic later.)
I will start by taking the Mover class from Chapter 2 examples and renaming it Rocket.
class Rocket {
constructor(x, y){
// A rocket has three vectors: position, velocity, acceleration.
this.position = createVector(x, y);
this.velocity = createVector();
this.acceleration = createVector();
}
// Accumulating forces into acceleration (Newton’s 2nd law)
applyForce(force) {
this.acceleration.add(force);
}
// A simple physics engine (Euler integration)
update() {
// Velocity changes according to acceleration.
this.velocity.add(this.acceleration);
//{!1} position changes according to velocity.
this.position.add(this.velocity);
this.acceleration.mult(0);
}
}
With the above class, I can implement a smart rocket by calling applyForce() with a new force for every frame of animation. The "thruster" applies a single force to the rocket each time through draw().
Before completing the rocket, however, let’s go through the three keys to programming a custom genetic algorithm example as outlined in the previous section.
I will hold off on this first key for now and arbitrarily choose some reasonable numbers (such as a population of 100 rockets and a mutation rate of 1%) and build the system out. Once I have my sketch up and running, I can experiment with these numbers.
I have defined the goal of a rocket as reaching its target. In other words, the closer a rocket gets to the target, the higher the fitness. Fitness is inversely proportional to distance: the smaller the distance, the greater the fitness; the greater the distance, the smaller the fitness.
Assuming I have a target vector, I can calculate fitness as follows.
calculateFitness() {
// How close did the rocket get?
let distance = p5.Vector.dist(this.position, target);
//{!1} Fitness is inversely proportional to distance.
this.fitness = 1 / distance;
}
This is perhaps the simplest fitness function I could write. By dividing one by the distance, large distances become small numbers and small distances become large. And if I wanted to use my quadratic trick from the previous section, I could use one divided by distance squared.
There are several additional improvements I'll want to make to the fitness function, but this is a good start.
calculateFitness() {
let distance = p5.Vector.dist(position, target);
//{!1} 1 divided by distance squared
this.fitness = 1 / (distance * distance);
}
I stated that each rocket has a thruster that fires in a variable direction with a variable magnitude, in other words, a vector! The genotype, the data required to encode the rocket’s behavior, is therefore an array of vectors.
class DNA {
constructor(length) {
this.genes = [];
for (let i = 0; i < length; i++) {
this.genes[i] = createVector();
}
}
}
The happy news here is that I don’t really have to do anything else to the DNA class. All of the functionality for the typing monkey (crossover and mutation) applies here. The one difference I do have to consider is how to initialize the array of genes. With the typing monkey, I had an array of characters and picked a random character for each element of the array. Here I'll do exactly the same thing and initialize a DNA sequence as an array of random vectors. Now, your instinct in creating a random vector might be as follows:
let v = createVector(random(-1, 1), random(-1, 1));

This is perfectly fine and will likely do the trick. However, if I were to draw every single possible vector I might pick, the result would fill a square (see Figure 9.12). In this case, it probably doesn’t matter, but there is a slight bias to the diagonals given that a vector from the center of a square to a corner is longer than a purely vertical or horizontal one.

What would be better here is to pick a random angle and make a vector of length one from that angle, giving us a circle (see Figure 9.13). This could be done with a quick Polar to Cartesian conversion, but a quicker path to the result is just to use p5.Vector.random2D().
for (let i = 0; i < length; i++) {
//{!1} A random unit vector
this.genes[i] = p5.Vector.random2D();
}
A vector of length one would actually create quite a large force. Remember, forces are applied to acceleration, which accumulates into velocity thirty times per second (or whatever the frame rate is). Therefore, for this example, I will add another variable to the DNA class: a maximum force that scales all the vectors. This will control the thruster power.
class DNA {
constructor() {
// The genetic sequence is an array of vectors.
this.genes = [];
// How strong can the thrusters be?
this.maxForce = 0.1;
// notice that length of genes is equal to a global variable "lifeSpan"
for (let i = 0; i < lifeSpan; i++) {
this.genes[i] = p5.Vector.random2D();
//{!1} Scaling the vectors randomly, but no stronger than maximum force
this.genes[i].mult(random(0, maxforce));
}
}
Notice also that I created the array of vectors genes with the length lifeSpan. I need a vector for each frame of the rocket’s life, and the above assumes the existence of a global variable that stores the total number of frames in each generation’s life cycle.
The expression of this array of vectors, the phenotype, is a Rocket class modeled on the forces examples from Chapter 2. All I need to do is add an instance of a DNA object to the class. The fitness will also be stored here. Only the Rocket object knows how to compute its distance to the target, and therefore the fitness function can live in the phenotype class.
class Rocket {
constructor(x, y, dna){
// A Rocket has DNA.
this.dna = dna;
// A Rocket has fitness.
this.fitness = 0;
this.position = createVector(x, y);
this.velocity = createVector();
this.acceleration = createVector();
}
What am I using this.dna for? As the rocket launches, it march through the array of vectors and apply them one at a time as a force. To achieve this, I'll need to include a variable this.geneCounter that acts as a counter to walk through the array.
class Rocket {
constructor(x, y, dna) {
// A Rocket has DNA.
this.dna = dna;
// A Rocket has fitness.
this.fitness = 0;
//{!1} A counter for the dna genes array
this.geneCounter = 0;
this.position = createVector(x, y);
this.velocity = createVector();
this.acceleration = createVector();
}
run() {
// Apply a force from the genes array.
this.applyForce(this.dna.genes[this.geneCounter]);
// Go to the next force in the genes array.
this.geneCounter++;
//{!1} Update the Rocket’s physics.
this.update();
}
}
Now I have a DNA class (genotype) and a Rocket class (phenotype). The last piece of the puzzle is a Population class, which manages an array of rockets and has the functionality for selection and reproduction. Again, the happy news here is that I barely have to change anything from the Shakespeare monkey example. The process for building a mating pool and generating a new array of child rockets is exactly the same as what I did with our population of strings. This time, however, just to demonstrate a different technique, I’ll normalize the fitness values in the selection() function and use the weightedSelection() algorithm in reproduction(). This also eliminates the need for a separate “mating pool” array. The code for weighted selection is the same as what was written earlier in the chapter.
class Population {
// Population has variables to keep track of mutation rate, current
// population array and number of generations.
constructor(mutation, length) {
this.mutationRate = mutation; // Mutation rate
this.population = []; // Array to hold the current population
this.matingPool = []; // ArrayList which we will use for our "mating pool"
this.generations = 0; // Number of generations
for (let i = 0; i < length; i++) {
this.population[i] = new Rocket(320, 220, new DNA());
}
}
// The selection function now normalizes all the fitness values
selection() {
// Sum all of the fitness values
let totalFitness = 0;
for (let i = 0; i < this.population.length; i++) {
totalFitness += this.population[i].fitness;
}
// Divide by the total to normalize the fitness values
for (let i = 0; i < this.population.length; i++) {
this.population[i].fitness /= totalFitness;
}
}
reproduction() {
// Separate array for the next generation
let newPopulation = [];
for (let i = 0; i < this.population.length; i++) {
//{!2} Now using the weighted selection algorithm
let parentA = this.weightedSelection();
let parentB = this.weightedSelection();
let child = parentA.crossover(parentB);
child.mutate(this.mutationRate);
// Rocket goes in the new population
newPopulation[i] = new Rocket(320, 240, child);
}
// Now the new population is the current one
this.population = newPopulation;
}
There is one more fairly significant change, however. With typing monkeys, a random phrase was evaluated as soon as it was created. The string of characters had no lifespan; it existed purely for the purpose of calculating its fitness. The rockets, however, need to live for a period of time before they can be evaluated; they need to be given a chance to make their attempt at reaching the target. Therefore, I need to add one more function to the Population class that runs the physics simulation itself. This is identical to what I did in the run() function of a particle system—update all the particle positions and draw them.
live () {
for (let i = 0; i < this.population.length; i++) {
//{!1} The run function takes care of the simulation, updates the rocket’s
// position and draws it to the canvas.
this.population[i].run();
}
}
Finally, I'm ready for setup() and draw(). Here, my primary responsibility is to implement the steps of the genetic algorithm in the appropriate order by calling the functions from the Population class.
population.fitness();
population.selection();
population.reproduction();
However, unlike the Shakespeare example, I don’t want to do this every frame. Rather, my steps work as follows:

// How many frames does a generation live for?
let lifeSpan = 500;
// Keeping track of the lifespan
let lifeCounter = 0;
// The population
let population;
function setup() {
createCanvas(640, 240);
//{!1} Step 1: Create the population. Try different values for
// the mutation rate and population size.
population = new Population(0.01, 50);
}
function draw() {
background(255);
// The revised genetic algorithm
if (lifeCounter < lifeSpan) {
// Step 2: The rockets live their life until lifeCounter reaches lifeSpan.
population.live();
lifeCounter++;
} else {
// When lifeSpan is reached, reset lifeCounter and evolve the next
// generation (Steps 3 and 4, selection and reproduction).
lifeCounter = 0;
population.fitness();
population.selection();
population.reproduction();
}
}
The above example works, but it isn’t particularly interesting. After all, the rockets simply evolve to having DNA with a bunch of vectors that point straight upwards. In the next example, I'm going to talk through two suggested improvements for the example and provide code snippets that implement these improvements.
Adding obstacles for rockets to avoid can make the system more complex and demonstrate the power of the evolutionary algorithm more effectively. I can easily create rectangular, stationary obstacles by implementing a class that stores the position and dimensions of each obstacle.
class Obstacle {
constructor(x, y, w, h) {
this.position = createVector(x, y);
this.w = w;
this.h = h;
}
I can also write a contains() function that will return true if a rocket has hit the obstacle, and false otherwise.
contains(spot) {
return (
spot.x > this.position.x &&
spot.x < this.position.x + this.w &&
spot.y > this.position.y &&
spot.y < this.position.y + this.h
);
}
If I create an array of obstacles, I can then have each rocket check to see if it has collided with an obstacle. If a collision occurs, the rocket can set a boolean flag to true. To achieve this, a function needs to be added to the Rocket class.
// This new function lives in the Rocket class and checks if a rocket has
// hit an obstacle.
checkObstacles(obstacles) {
for (let obstacle of obstacles) {
if (obstacle.contains(this.position)) {
this.hitObstacle = true;
}
}
}
If the rocket hits an obstacle, I will stop it from updating its position. The revised run() function now receives an obstacles array as a argument.
run(obstacles) {
// Stop the rocket if it's hit an obstacle or the target
if (!this.hitObstacle && !this.hitTarget) {
this.applyForce(this.dna.genes[this.geneCounter]);
this.geneCounter = (this.geneCounter + 1) % this.dna.genes.length;
this.update();
// Check if rocket hits an obstacle
this.checkObstacles(obstacles);
}
this.show();
}
I also have an opportunity to adjust the fitness of the rocket. If the rocket hits an obstacle, the fitness should be penalized and greatly reduced.
calculateFitness() {
let distance = p5.Vector.dist(this.position, target);
this.fitness = 1 / (distance * distance);
// {.bold !3}
if (this.hitObstacle) {
this.fitness *= 0.1;
}
}
If you look closely at the first Smart Rockets example, you’ll notice that the rockets are not rewarded for getting to the target faster. The only variable in the fitness calculation is the distance to the target at the end of the generation’s life. In fact, in the event that a rocket gets very close to the target but overshoots it and flies past, it may actually be penalized for getting to the target faster. Slow and steady wins the race in this case.
There are several ways in which I could improve the algorithm to optimize for speed to reach the target. First, I could use the distance that is closest to the target at any point during the rocket's life, instead of using the distance to the target at the end of the generation. I’ll call this variable the rocket's recordDistance. All of the code snippets in this section are enhancements to the Rocket class.
checkTarget() {
let distance = p5.Vector.dist(this.position, target);
//{!3} Check if the distance is closer than the “record” distance. If it is, set a new record.
if (distance < this.recordDistance) {
this.recordDistance = distance;
}
Additionally, a rocket should be rewarded based on how quickly it reaches its target. The faster it reaches the target, the higher its fitness score. Conversely, the slower it reaches the target, the lower its fitness score. To implement this, a finishCounter can be incremented every cycle of the rocket's life until it reaches the target. At the end of its life, the counter will equal the amount of time the rocket took to reach the target.
// If the object reaches the target, set a boolean flag to true.
if (target.contains(this.position) && !this.hitTarget) {
this.hitTarget = true;
// Otherwise, increase the finish counter
} else if (!this.hitTarget) {
this.finishCounter++;
}
}
Fitness is also inversely proportional to finishCounter. Therefore, I can improve the fitness function by doing the following:
calculateFitness() {
// Reward finishing faster and getting close
this.fitness = 1 / (this.finishTime * this.recordDistance);
// Let's try to the power of 4 instead of squared!
this.fitness = pow(this.fitness, 4);
//{!3} lose 90% of fitness hitting an obstacle
if (this.hitObstacle) {
this.fitness *= 0.1;
}
//{!3} Double the fitness for finishing!
if (this.hitTarget) {
this.fitness *= 2;
}
}
These improvements are both incorporated into the code for Example 9.3: Smart Rockets.
Create a more complex obstacle course. As you make it more difficult for the rockets to reach the target, do you need to improve other aspects of the GA—for example, the fitness function?
Implement the rocket firing pattern of Jer Thorp’s Smart Rockets. Each rocket only gets five thrusters (of any direction and strength) that follow a firing sequence (of arbitrary length). Jer’s simulation also gives the rockets a finite amount of fuel.
Visualize the rockets differently. Can you draw a line for the shortest path to the target? Can you add particle systems that act as smoke in the direction of the rocket thrusters?
Another way to achieve a similar result is to evolve a flow field. Can you make the genotype of a rocket a flow field of vectors?
One of the more famous implementations of genetic algorithms in computer graphics is Karl Sims’s “Evolved Virtual Creatures.” In Sims’s work, a population of digital creatures (in a simulated physics environment) is evaluated for the their ability to perform tasks, such as swimming, running, jumping, following, and competing for a green cube.
One of the innovations in Sims’s work is a node-based genotype. In other words, the creature’s DNA is not a linear list of vectors or numbers, but a map of nodes. (For an example of this, take a look at [TBD: Cross Reference Chapter 6]. The phenotype is the creature’s body itself, a network of limbs connected with muscles.
Using toxiclibs.js or matter.js as the physics model, can you create a simplified 2D version of Sims’s creatures? For a lengthier description of Sims’s techniques, you can read his 1994 Paper “Evolving Virtual Creatures.”

In addition to Evolving Virtual Creatures, Sims is also well known for his museum installation Galapagos. Originally installed in the Intercommunication Center in Tokyo in 1997, the installation consists of twelve monitors displaying computer-generated images. These images evolve over time, following the genetic algorithm steps of selection and reproduction. The innovation here is not the use of the genetic algorithm itself, but rather the strategy behind the fitness function. In front of each monitor is a sensor on the floor that can detect the presence of a visitor viewing the screen. The fitness of an image is tied to the length of time that viewers look at the image. This is known as interactive selection, a genetic algorithm with fitness values assigned by people.
Think of all the rating systems you’ve ever used. Could you evolve the perfect movie by scoring all films according to your Netflix ratings? The perfect singer according to American Idol voting?

To illustrate this technique, I'm going to build a population of simple faces. Each face will have a set of properties: head size, head color, eye position, eye size, mouth color, mouth position, mouth width, and mouth height.
The face’s DNA (genotype) is an array of floating point numbers between 0 and 1, with a single value for each property.
class DNA {
constructor(newgenes) {
// DNA is random floating point values between 0 and 1 (!!)
// The genetic sequence
let len = 20; // Arbitrary length
if (newgenes) {
this.genes = newgenes;
} else {
this.genes = new Array(len);
for (let i = 0; i < this.genes.length; i++) {
this.genes[i] = random(0, 1);
}
}
}
The phenotype is a Face class that includes an instance of a DNA object.
class Face {
constructor(dna){
this.dna = dna; // Face's DNA
this.fitness = 1; // How good is this face?
}
When it comes time to draw the face on screen, I will use p5.js’s map() function to convert any gene value to the appropriate range for pixel dimensions or color values. (In this case, we are also using colorMode() to set the RGB ranges between 0 and 1.)
display() {
//{.offset-top} Using map() to convert the genes to a range for drawing the face.
// We are using the face's DNA to pick properties for this face
// such as: head size, color, eye position, etc.
let genes = this.dna.genes;
let r = map(genes[0], 0, 1, 0, 70);
let c = color(genes[1], genes[2], genes[3]);
let eye_y = map(genes[4], 0, 1, 0, 5);
let eye_x = map(genes[5], 0, 1, 0, 10);
let eye_size = map(genes[5], 0, 1, 0, 10);
let eyecolor = color(genes[4], genes[5], genes[6]);
let mouthColor = color(genes[7], genes[8], genes[9]);
let mouth_y = map(genes[5], 0, 1, 0, 25);
let mouth_x = map(genes[5], 0, 1, -25, 25);
let mouthw = map(genes[5], 0, 1, 0, 50);
let mouthh = map(genes[5], 0, 1, 0, 10);
So far, I'm not really doing anything new. This is what I've done in every GA example so far. What’s new is that I'm are not going to write a fitness() function in which the score is computed based on a math formula. Instead, I am going to ask the user to assign the fitness.
Now, how best to ask a user to assign fitness is really more of an interaction design problem, and it isn’t really within the scope of this book. So I'm not going to launch into an elaborate discussion of how to program sliders or build your own hardware dials or build a Web app for users to submit online scores. How you choose to acquire fitness scores is really up to you and the particular application you are developing.
For this simple demonstration, I'll increase fitness whenever a user rolls the mouse over a face. The next generation is created when the user presses a button with an “evolve next generation” label.
Look at how the steps of the genetic algorithm are applied in the sketch.js file, noting how fitness is assigned according to mouse interaction and the next generation is created on a button press. The rest of the code for checking mouse positions, button interactions, etc. can be found in the accompanying example code.
let population;
let info;
function setup() {
createCanvas(800, 124);
colorMode(RGB, 1.0, 1.0, 1.0, 1.0);
let popmax = 10;
let mutationRate = 0.05; // A pretty high mutation rate here, our population is rather small we need to enforce variety
// Create a population with a target phrase, mutation rate, and population max
population = new Population(mutationRate, popmax);
// A simple button class
button = createButton("evolve new generation");
button.mousePressed(nextGen);
button.position(10, 140);
info = createDiv('');
info.position(10, 175);
}
function draw() {
background(1);
// Display the faces
population.display();
population.rollover(mouseX, mouseY);
info.html("Generation #:" + population.getGenerations());
}
// If the button is clicked, evolve next generation
function nextGen() {
population.selection();
population.reproduction();
}
This example, it should be noted, is really just a demonstration of the idea of interactive selection and does not achieve a particularly meaningful result. For one, I didn’t take much care in the visual design of the faces; they are just a few simple shapes with sizes and colors. Sims, for example, used more elaborate mathematical functions as his images’ genotype. You might also consider a vector-based approach, in which a design’s genotype is a set of points and/or paths.
The more significant problem here, however, is one of time. In the natural world, evolution occurs over millions of years. In the computer simulation world in the previous examples, the populations are able to evolve behaviors relatively quickly because you are producing new generations algorithmically. In the Shakespeare monkey example, a new generation was born in each frame of animation (approximately sixty per second). Since the fitness values were computed according to a math formula, you could also have had arbitrarily large populations that increased the speed of evolution. In the case of interactive selection, however, you have to sit and wait for a user to rate each and every member of the population before you can get to the next generation. A large population would be unreasonably tedious to deal with—not to mention, how many generations could you stand to sit through?
There are certainly clever solutions around this. Sims’s Galapagos exhibit concealed the rating process from the users, as it occurred through the normal behavior of looking at artwork in a museum setting. Building a Web application that would allow many users to rate a population in a distributed fashion is also a good strategy for achieving many ratings for large populations quickly.
In the end, the key to a successful interactive selection system boils down to the same keys we previously established. What is the genotype and phenotype? And how do you calculate fitness, which in this case we can revise to say: “What is your strategy for assigning fitness according to user interaction?”
Build your own interactive selection project. In addition to a visual design, consider evolving sounds—for example, a short sequence of tones. Can you devise a strategy, such as a Web application or physical sensor system, to acquire ratings from many users over time?
You may have noticed something a bit odd about every single evolutionary system you've built so far in this chapter. After all, in the real world, a population of babies isn’t born all at the same time. Those babies don’t then grow up and all reproduce at exactly the same time, then instantly die to leave the population size perfectly stable. That would be ridiculous. Not to mention the fact that there is certainly no one running around the forest with a calculator crunching numbers and assigning fitness values to all the creatures.
In the real world, you don’t really have “survival of the fittest”; you have “survival of the survivors.” Things that happen to live longer, for whatever reason, have a greater chance of reproducing. Babies are born, they live for a while, maybe they themselves have babies, maybe they don’t, and then they die.
You won’t necessarily find simulations of “real-world” evolution in artificial intelligence textbooks. Genetic algorithms are generally used in the more formal manner we outlined in this chapter. However, since you are reading this book to develop simulations of natural systems, it’s worth looking at some ways in which you might use a genetic algorithm to build something that resembles a living “ecosystem,” much like the one I've described in the exercises at the end of each chapter.
I'll begin by developing a very simple scenario. I'll create a creature called a "bloop," a circle that moves about the screen according to Perlin noise. The creature will have a radius and a maximum speed. The bigger it is, the slower it moves; the smaller, the faster.
class Bloop {
constructor(l, dna) {
this.position = l.copy(); // Location
this.xoff = random(1000); // For perlin noise
this.yoff = random(1000);
this.dna = dna; // DNA
// DNA will determine size and maxspeed
// The bigger the bloop, the slower it is
this.maxspeed = map(this.dna.genes[0], 0, 1, 15, 0);
this.r = map(this.dna.genes[0], 0, 1, 0, 50);
}
update() {
float vx = map(noise(xoff), 0, 1, -maxspeed, maxspeed);
float vy = map(noise(yoff), 0, 1, -maxspeed, maxspeed);
//{!1} A little Perlin noise algorithm to calculate a velocity
PVector velocity = new PVector(vx, vy);
xoff += 0.01;
yoff += 0.01;
//{!1} The bloop moves.
position.add(velocity);
}
//{!3} A bloop is a circle.
display() {
ellipseMode(CENTER);
ellipse(this.position.x, this.position.y, this.r, this.r);
}
}
The above is missing a few details (such as initializing the variables in the constructor), but you get the idea.
For this example, you'll want to store the population of bloops in an array, rather than an array, as you expect the population to grow and shrink according to how often bloops die or are born. You can store this array in a class called World, which will manage all the elements of the bloops’ world.
class World {
//{!1} A list of bloops
constructor(num) {
// Start with set of creatures
this.bloops = []; // An array for all creatures
for (let i = 0; i < num; i++) {
let l = createVector(random(width), random(height));
let dna = new DNA();
this.bloops.push(new Bloop(l, dna));
}
}
So far, what I have is just a rehashing of our particle system example from Chapter 5. I have an entity (Bloop) that moves around the window and a class (World) that manages a variable quantity of these entities. To turn this into a system that evolves, I'll need to add two additional features to my world:
Bloops dying is my replacement for a fitness function, the process of “selection.” If a bloop dies, it cannot be selected to be a parent, because it simply no longer exists! One way I can build a mechanism to ensure bloop deaths in our world is by adding a health variable to the Bloop class.
class Bloop {
constructor(l, dna_) {
this.position = l.copy(); // Location
//{!1} A bloop is born with 100 health points.
this.health = 100; // Life timer
this.xoff = random(1000); // For perlin noise
this.yoff = random(1000);
this.dna = dna_; // DNA
// DNA will determine size and maxspeed
// The bigger the bloop, the slower it is
this.maxspeed = map(this.dna.genes[0], 0, 1, 15, 0);
this.r = map(this.dna.genes[0], 0, 1, 0, 50);
}
In each frame of animation, a bloop loses some health.
update() {
// Simple movement based on perlin noise
let vx = map(noise(this.xoff), 0, 1, -this.maxspeed, this.maxspeed);
let vy = map(noise(this.yoff), 0, 1, -this.maxspeed, this.maxspeed);
let velocity = createVector(vx, vy);
this.xoff += 0.01;
this.yoff += 0.01;
this.position.add(velocity);
// Death always looming
this.health -= 0.2;
}
If health drops below 0, the bloop dies.
// We add a function to the Bloop class
// to test if the bloop is alive or dead.
dead() {
if (this.health < 0.0) {
return true;
} else {
return false;
}
}
This is a good first step, but I haven’t really achieved anything. After all, if all bloops start with 100 health points and lose 1 point per frame, then all bloops will live for the exact same amount of time and die together. If every single bloop lives the same amount of time, they all have equal chances of reproducing and therefore nothing will evolve.
There are many ways I could achieve variable lifespans with a more sophisticated world. For example, I could introduce predators that eat bloops. Perhaps the faster bloops would be able to escape being eaten more easily, and therefore our world would evolve to have faster and faster bloops. Another option would be to introduce food. When a bloop eats food, it increases its health points, and therefore extends its life.
Let’s assume I have an array of vector positions for food, named “food.” We could test each bloop’s proximity to each food position. If the bloop is close enough, it eats the food (which is then removed from the world) and increases its health.
eat(f) {
let food = f.getFood();
// Are we touching any food objects?
for (let i = food.length - 1; i >= 0; i--) {
let foodLocation = food[i];
let d = p5.Vector.dist(this.position, foodLocation);
// If we are, juice up our strength!
if (d < this.r / 2) {
this.health += 100;
//{!1} The food is no longer available for other Bloops.
food.splice(i, 1);
}
}
}
Now I have a scenario in which bloops that eat more food live longer and have a greater likelihood of reproducing. Therefore, I expect that our system would evolve bloops with an optimal ability to find and eat food.
Now that I have built our world, it’s time to add the components required for evolution. First I should establish our genotype and phenotype.
The ability for a bloop to find food is tied to two variables—size and speed. Bigger bloops will find food more easily simply because their size will allow them to intersect with food positions more often. And faster bloops will find more food because they can cover more ground in a shorter period of time.
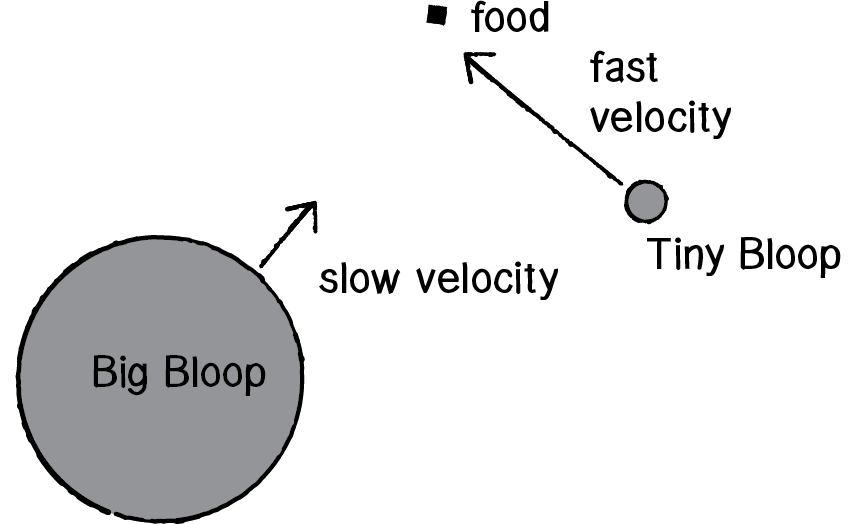
Since size and speed are inversely related (large bloops are slow, small bloops are fast), I only need a genotype with a single number.
class DNA {
constructor(newgenes) {
if (newgenes) {
this.genes = newgenes;
} else {
// The genetic sequence
// DNA is random floating point values between 0 and 1 (!!)
this.genes = new Array(1);
for (let i = 0; i < this.genes.length; i++) {
this.genes[i] = random(0, 1);
}
}
}
The phenotype then is the bloop itself, whose size and speed is assigned by adding an instance of a DNA object to the Bloop class.
class Bloop {
constructor(l, dna) {
this.position = l.copy(); // Location
this.health = 200; // Life timer
this.xoff = random(1000); // For perlin noise
this.yoff = random(1000);
this.dna = dna; // DNA
// DNA will determine size and maxspeed
// The bigger the bloop, the slower it is
this.maxspeed = map(this.dna.genes[0], 0, 1, 15, 0);
this.r = map(this.dna.genes[0], 0, 1, 0, 50);
}
Notice that with maxspeed, the range is mapped to between 15 and 0, meaning a bloop with a gene value of 0 moves at a speed of 15 and a bloop with a gene value of 1 doesn’t move at all (speed of 0).
Now that I have the genotype and phenotype, I need to move on to devising a means for bloops to be selected as parents. I stated before that the longer a bloop lives, the more chances it has to reproduce. The length of life is the bloop’s fitness.
One option would be to say that whenever two bloops come into contact with each other, they make a new bloop. The longer a bloop lives, the more likely it is to come into contact with another bloop. (This would also affect the evolutionary outcome given that, in addition to eating food, their ability to find other bloops is a factor in the likelihood of having a baby.)
A simpler option would be to have “asexual” reproduction, meaning a bloop does not require a partner. It can, at any moment, make a clone of itself, another bloop with the same genetic makeup. If I state this selection algorithm as follows:
At any given moment, a bloop has a 1% chance of reproducing.
…then the longer a bloop lives, the more likely it will make at least one child. This is equivalent to saying the more times you play the lottery, the greater the likelihood you’ll win (though I’m sorry to say your chances of that are still essentially zero).
To implement this selection algorithm, I can write a function in the Bloop class that picks a random number every frame. If the number is less than 0.01 (1%), a new bloop is born.
// This function will return a new bloop, the child.
reproduce() {
// A 1% chance of executing the code in
// this conditional, i.e. a 1% chance of reproducing
if (random(1) < 0.01) {
[inline] // Make the Bloop baby
}
}
How does a bloop reproduce? In our previous examples, the reproduction process involved calling the crossover() function in the DNA class and making a new object from the newly made DNA. Here, since I am making a child from a single parent, I'll call a function called copy() instead.
reproduce() {
// asexual reproduction
if (random(1) < 0.0005) {
// Child is exact copy of single parent
let childDNA = this.dna.copy();
// Child DNA can mutate
childDNA.mutate(0.01);
return new Bloop(this.position, childDNA);
} else {
return null;
}
}
Note also that I've reduced the probability of reproducing from 1% to 0.05%. This value makes quite a difference; with a high probability of reproducing, the system will quickly tend towards overpopulation. Too low a probability, and everything will likely quickly die out.
Writing the copy() function into the DNA class is easy since p5.js includes a function arraycopy() that copies the contents of one array into another.
class DNA {
//{!1} This copy() function replaces
// crossover() in this example.
copy() {
// should switch to fancy JS array copy
let newgenes = [...this.genes];
return new DNA(newgenes);
}
}
Now that I have all the pieces in place for selection and reproduction, I can finalize the World class that manages the list of all Bloop objects (as well as a Food object, which itself is a list of vector positions for food).
Before you run the example, take a moment to guess what size and speed of bloops the system will evolve towards. I'll discuss following the code.
let world;
function setup() {
createCanvas(640, 360);
// World starts with 20 creatures
// and 20 pieces of food
world = new World(20);
}
function draw() {
background(175);
world.run();
}
class World {
//{!2} The World object keeps track of the
// population bloops as well as the food.
constructor(num) {
// Start with initial food and creatures
this.food = new Food(num);
this.bloops = []; // An array for all creatures
for (let i = 0; i < num; i++) {
let l = createVector(random(width), random(height));
let dna = new DNA();
//{!4 .offset-top} Creating the population
this.bloops.push(new Bloop(l, dna));
}
}
// Make a new creature
born(x, y) {
let l = createVector(x, y);
let dna = new DNA();
this.bloops.push(new Bloop(l, dna));
}
// Run the world
run() {
// Deal with food
this.food.run();
// Cycle through the ArrayList backwards b/c we are deleting
for (let i = this.bloops.length - 1; i >= 0; i--) {
// All bloops run and eat
let b = this.bloops[i];
b.run();
b.eat(this.food);
// If it's dead, kill it and make food
if (b.dead()) {
this.bloops.splice(i, 1);
this.food.add(b.position);
}
// Perhaps this bloop would like to make a baby?
//{!2} Here is where each living bloop has
// a chance to reproduce. As long as a
// child is made (i.e. not null) it is
// added to the population.
let child = b.reproduce();
if (child != null) this.bloops.push(child);
}
}
}
If you guessed medium-sized bloops with medium speed, you were right. With the design of this system, bloops that are large are simply too slow to find food. And bloops that are fast are too small to find food. The ones that are able to live the longest tend to be in the middle, large enough and fast enough to find food (but not too large or too fast). There are also some anomalies. For example, if it so happens that a bunch of large bloops end up in the same position (and barely move because they are so large), they may all die out suddenly, leaving a lot of food for one large bloop who happens to be there to eat and allowing a mini-population of large bloops to sustain themselves for a period of time in one position.
This example is rather simplistic given its single gene and asexual reproduction. Here are some suggestions for how you might apply the bloop example in a more elaborate ecosystem simulation.
Step 9 Exercise:
Add evolution to your ecosystem, building from the examples in this chapter.